Then multiplying the numerator and denominator inside the square root by (1 cos θ) and using Pythagorean identities leads to = Also, if the numerator and denominator are both multiplied by (1 cos θ), the result is = This also gives = Similar manipulations for the cot function give = = = = Miscellaneou10th maths introduction to trignometry ncert solution1 tan²θ = sec²θ or tan²θ = sec²θ – 1 on expanding tan²θ = ( x1/4x)² 1 or tan²θ = ( x² 1/16x² 1/2 – 1) or tan²θ = (x² 1/16x² – 1/2) or tan²θ = x² 1/16x² – 1/2 or tan²θ = (x – 1/4x) 2 or tanθ = (x1/4x) or – (x1/4x) when tanθ = (x1/4x) we get secθ tanθ = x 1/4x x 1/4x = 2x
What Is Tan 2 Theta Equal To
Tan 2 theta is equal to 2 tan theta upon 1 minus 10 squared theta
Tan 2 theta is equal to 2 tan theta upon 1 minus 10 squared theta-Click here👆to get an answer to your question ️ If tantheta sintheta = m, tantheta sintheta = n and m≠ n , then show that m^2 n^2 = 4√(mn)Notice, math7\sin^2\theta3\cos^2\theta=4/math math\frac{7\tan^2\theta}{\sec^2\theta}\frac{3}{\sec^2\theta}=4/math math\frac{7\tan^2\theta3}{\sec^2\theta


Prove That 2 Tan2 Cot2 Tan Cot Mathematics Topperlearning Com Ttevdk55
· How do you prove #\csc \theta \times \tan \theta = \sec \theta#? · cosecant of angle θ = cosecθ = Hypotenuse Perpendicular secant of angle θ = secθ = Hypotenuse Base Note that, sine, cosine, tangent, cotangent, cosecant, and secant are called Trigonometric Functions that defines the relationship between the sides and angles of the triangleCosine squared plus sine squared equals 1 can also be written cosine squared theta equals 1 minus sine squared theta or sine squared theta equals 1 minus cosine squared theta Now the original cosine double angle formula is this, cosine of 2 theta equals cosine squared theta minus sine squared theta, but I can use my Pythagorean identities to rewrite this, so another form
I hope this video helpful to you, if Yes!So, in either case, the result can never be equal to 2 The final result would be ,sin^2 (theta)cos^2 (theta)=1–2cos^2 (theta) and this is also a well known and widely used trigonometric identity After squaring both terms will become positive , so we are subtracting a positive number by aSolution 2Show Solution ⇒ ` (1 sin θ)^2/cos^2 θ = P^2`, (Squaring both sides) ⇒ ` (1 sin^2 θ 2 sin θ cos^2 θ)/ (1 sin^2 θ 2 sin θ cos^2 θ) = (p^2 1)/ (p^2 1)` (Applying componendo and dividendo ⇒ ` (1 1 2 sin θ)/ (sin^2 θ sin^2 θ 2 sin θ) = (p^2 1)/ (p^2 1)` Hence proved
Solution (TanX)(CotX)=1 its a formula Tan6ACot6A if equal to 1 Then Tan6ATan3A equal to Tan6ACot6A Divide with Tan6A bothFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor$\tan^2{\theta} \,=\, \sec^2{\theta}1$ The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity Introduction The tangent functions are often involved in trigonometric expressions and equations in square form The expressions or equations can be possibly simplified by transforming the tan squared


What Is Tan Squared Theta Equal To
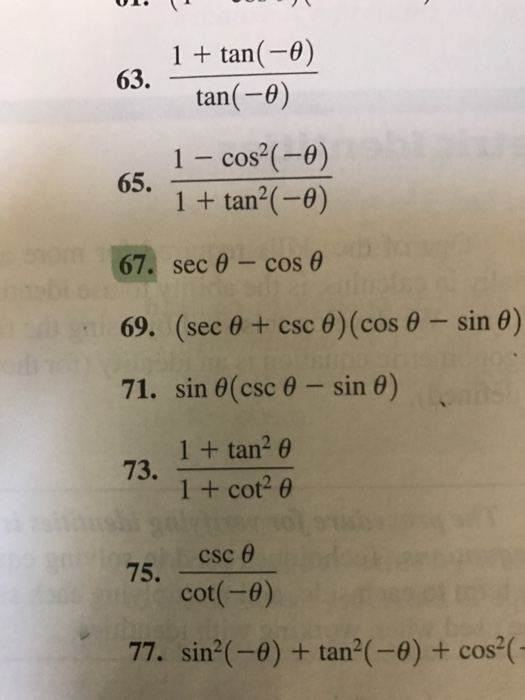


Solved 1 Tan Theta Tan Theta 1 Cos 2 Theta 1 Tan 2 Chegg Com
Click here👆to get an answer to your question ️ If sintheta sin^2 theta = 1 , what is the value of cos^2 theta cos^4 theta ?Introduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formulaLHS {tex}\tan \left {{\pi \over 4} {1 \over 2}{{\cos }^{ 1}}{a \over b}} \right \tan \left {{\pi \over 4} {1 \over 2}{{\cos }^{ 1}}{a \over b}} \right



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



If Tan Theta Sec Theta 2 Then What Is Tan Theta Is Equal To Quora
Tan 3 theta = 3 tan theta – tan 3 theta / 1 – 3 tan 2 theta Where tan is a tangent function and theta is an angle This is one of the important trigonometry formulas Tan 3x Formula Example Question If Tan6ATan3A=1, then what is the value of A?Click here👆to get an answer to your question ️ Prove that (cosec theta cot theta)^2 = 1 cos theta1 cos thetaFree math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantly



Prove That 1 Tan Theta Upon 1 Cot Theta 1 Tan Theta Upon 1 Cot Theta Brainly In


What Is Tan 2 Theta Equal To
Tan (θ) = −√3 tan ( θ) = 3 Take the inverse tangent of both sides of the equation to extract θ θ from inside the tangent θ = arctan(−√3) θ = arctan ( 3) The exact value of arctan(−√3) arctan ( 3) is − π 3 π 3 θ = − π 3 θ = π 3 The tangent function is negative inSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreTan (or tg) opposite / adjacent One has () = for j = 1, 2 The quotient rule implies thus that (() ()) = In words the theorem is the cotangent of a halfangle equals the ratio of the semiperimeter minus the opposite side to the said angle, to the inradius for the triangle A Lissajous curve, a figure formed with a trigonometrybased function Periodic functions An animation of the



Prove That Tan 2 Theta Sin 2 Theta Tan 2 Theta Sin 2 Theta



Sin 2 Theta Is Equal To 2 Tan Theta Upon 1 Tan Square Theta And Theta 30 Degree Brainly In
In trigonometrical ratios of angles (180° θ) we will find the relation between all six trigonometrical ratios · Prove that 1 tan squared theta upon 1 cot squared theta is equals to 1 minus 10 theta upon 1 minus cot theta square is equals to tan square thetaTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If `3 sin theta 4 cos theta =5` then `4 sin theta 3cos theta` is equal to


What Is Tan Squared Theta Minus One
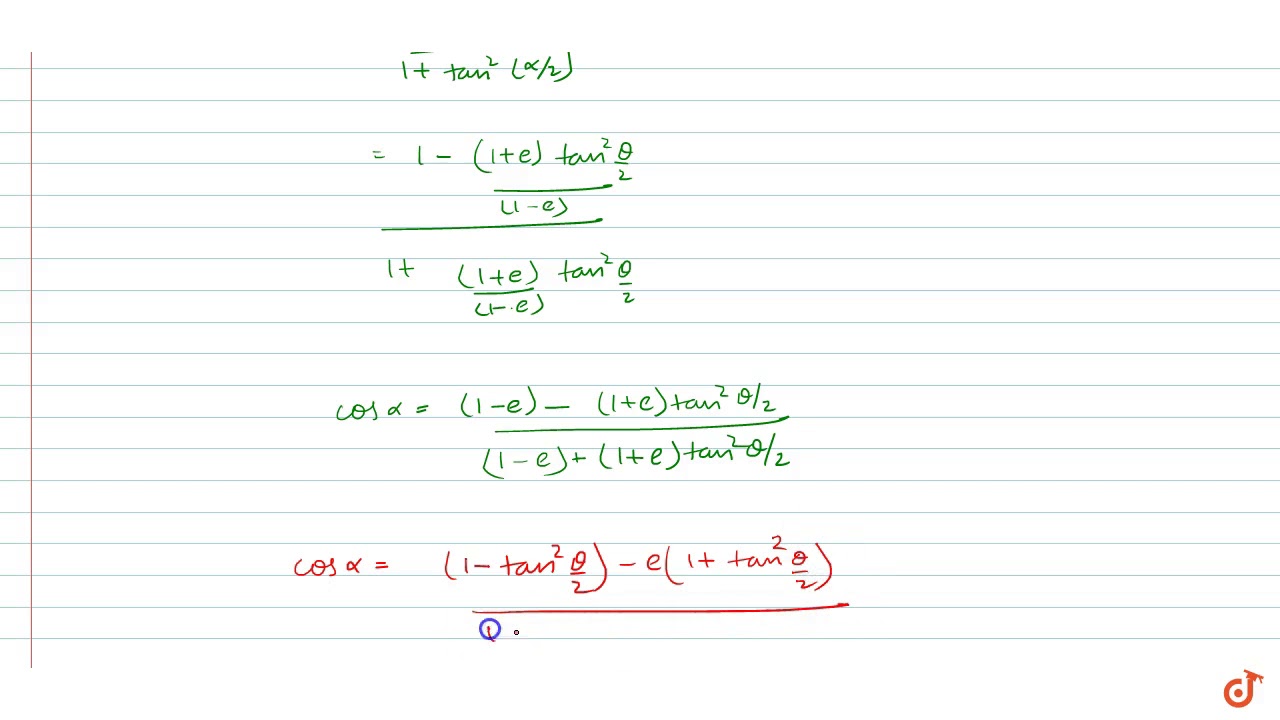


If Tan Theta 2 Sqrt 1 E 1 E Tan Alpha 2 Then Cos Alpha Youtube
· Let the side adjacent theta (the one we would like to find) be b a^2 b^2 = c^2 b^2 = c^2 a^2 b = sqrt(c^2 a^2) b = sqrt(3^2 1^2) b = sqrt(9 1) b = sqrt(8) b = 2sqrt(2) Now here's where the diagram is really useful Since the problem, doesn't specify a quadrant, we have to determine all quadrants where sine is negative The question we must ask ourselves is Where isThere will be several formulas of expressing math1sin\theta/math Firstly mathsin\theta \implies cos\theta/math mathsin^2\theta=1cos^2\theta/math mathAnswer to Find the exact value of tan(\theta) given cos (\theta) = \dfrac{1}{5}, \ 90^o < 0 < 180^o By signing up, you'll get thousands of



If 1 Sin 3 Sin Cos Then Show That Tan 1 Or 1 2 Mathematics Topperlearning Com 328h6ymm


What Is The Value Of Tan Theta If Sin Theta Cos Theta Root 2 Cos Theta Quora
Tan Theta formula The law of Tangent which is also called as tangent formula or tangent rule is the ratio of the sine of the angle to the cos of the angle Tan Θ = Opposite / AdjacentWhat are the relations among all the trigonometrical ratios of (180° θ)?Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor



If Sin 8 Cos 8 Then Find The Value Of 2 Tan 8 Cos 2 8 Teachoo



Sec 4 Theta 1 Sin 4 Theta 2tan Square Theta 1 Important Board Question Youtube
How do you prove #(1\cos^2 x)(1\cot^2 x) = 1#?How do you prove the following trigonometric identity $$ \sin^2\theta\cos^2\theta=1$$ I'm curious to know of the different ways of proving this depending on · (1 1/tan^2 theta)( 1 1/cot^2 theta) = 1/sin^2 theta sin^4 theta Get the answers you need, now!


If Cos Theta 5 13 Theta In Quadrant Ii How Do You Find Sin Theta And Tan Theta Socratic



Questions And Answers Cbse Icse Solutions Cbse Icse Study Materials Online Learning Question Papers Classnotes Practice Test Mcq
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorSorry if my question seems too simple I cannot find a proof and my text book does not provide one either I am supposed to prove $$\tan \theta \times \sin \theta \cos \theta = \sec \theta$$ I · Prove that (1 1/ tan2theta) (1 1/cot2theta) = 1/sin2theta sin4theta Maths Introduction to Trigonometry
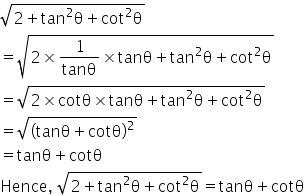


Prove That 2 Tan2 Cot2 Tan Cot Mathematics Topperlearning Com Ttevdk55



Prove That Sin Theta 2 Sin Cube Theta 2 Cos Cube Theta Minus Cos Theta Tan Theta Edurev Class 10 Question
The Chebyshev method is a recursive algorithm for finding the n th multiple angle formula knowing the (n − 1) th and (n − 2) th values cos(nx) can be computed from cos((n − 1)x), cos((n − 2)x), and cos(x) with cos(nx) = 2 · cos x · cos((n − 1)x) − cos((n − 2)x) This can be proved by adding together the formulaeI hope this video helpful to you and you like this video Please subscribe my channel and press the bell icon Like CommentWhich, upon division gives on the unit circle, draw the line passing through it and the point (−1, 0) This point crosses the yaxis at some point y = t One can show using simple geometry that t = tan(φ/2) The equation for the drawn line is y = (1 x)t The equation for the intersection of the line and circle is then a quadratic equation involving t The two solutions to this


How To Prove That Tan Theta Sec Theta 1 Sec Theta 1 Tan Theta Quora



If A 2 Sec 2 Theta B 2 Tan 2 Theta C 2 Prove That Sin Theta Plusmn Mathematics Topperlearning Com Q5azu9oo
Like this video and subscribe my channel and press the bell icon for more updatesyadi aapko kisi bHow do you show that #2 · The smallangle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians sin θ ≈ θ cos θ ≈ 1 − θ 2 2 ≈ 1 tan θ ≈ θ {\displaystyle {\begin{aligned}\sin \theta &\approx \theta \\\cos \theta &\approx 1{\frac {\theta ^{2}}{2}}\approx 1\\\tan \theta &\approx \theta



Prove It Sec Theta Tan Theta 1 Sec Theta Tan Theta 1 2tan Theta Brainly In


Prove That 2 Tan2 Cot2 Tan Cot Mathematics Topperlearning Com Ttevdk55
Move the limit inside the trig function because sine is continuous sin ( lim θ → 0 θ) lim θ → 0 θ sin ( lim θ → 0 θ) lim θ → 0 θ Evaluate the limit of θ θ by plugging in 0 0 for θ θ sin ( 0) lim θ → 0 θ sin ( 0) lim θ → 0 θ The exact value of sin ( 0) sin ( 0) is 0 0 0 lim θ → 0 θ 0 lim θ → 0 θ
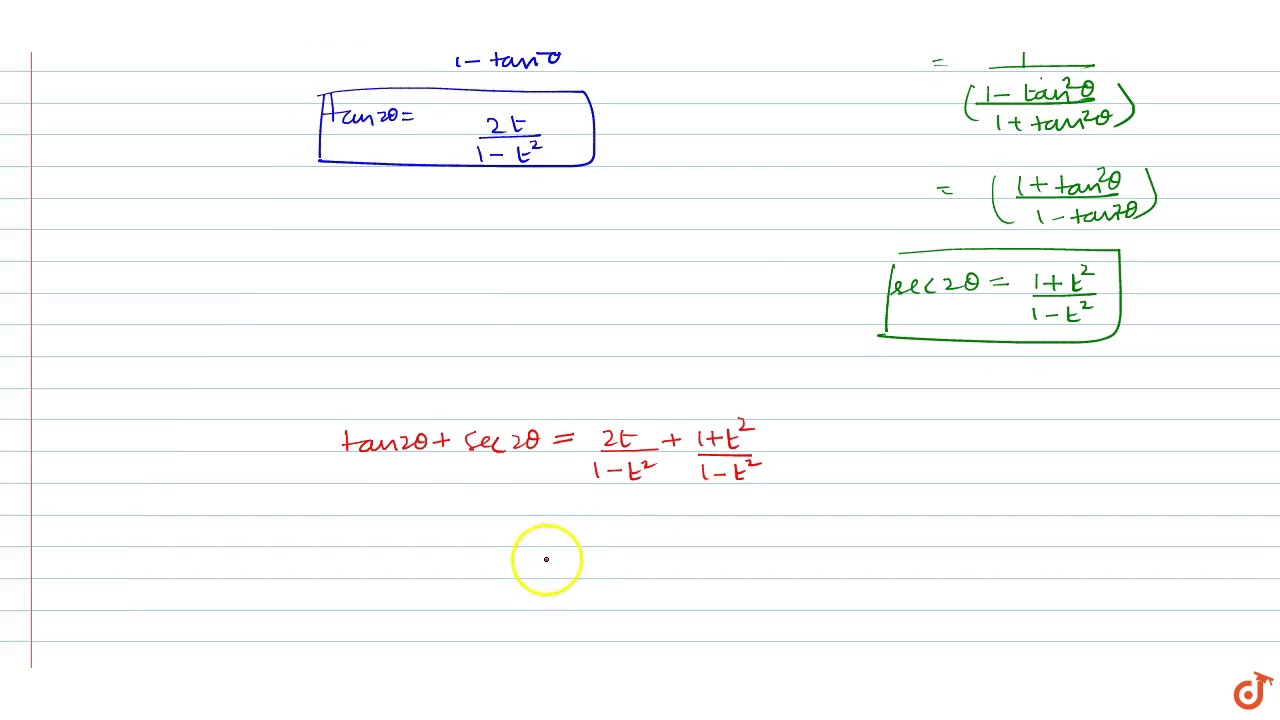


If Tan Theta T Then Tan 2 Theta Sec 2 Theta Youtube



If Theta 30 Verify That Tan 2theta 2 Tan Theta 1 Tan Square Theta Maths Introduction To Trigonometry Meritnation Com



Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com



If Theta 60 Then 1 Tan Square Theta 2tan Theta Is Equal To Brainly In



Find The Value Of Tan 2 Theta



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Solved Prove The The Following Identity Tan 2 Theta Chegg Com
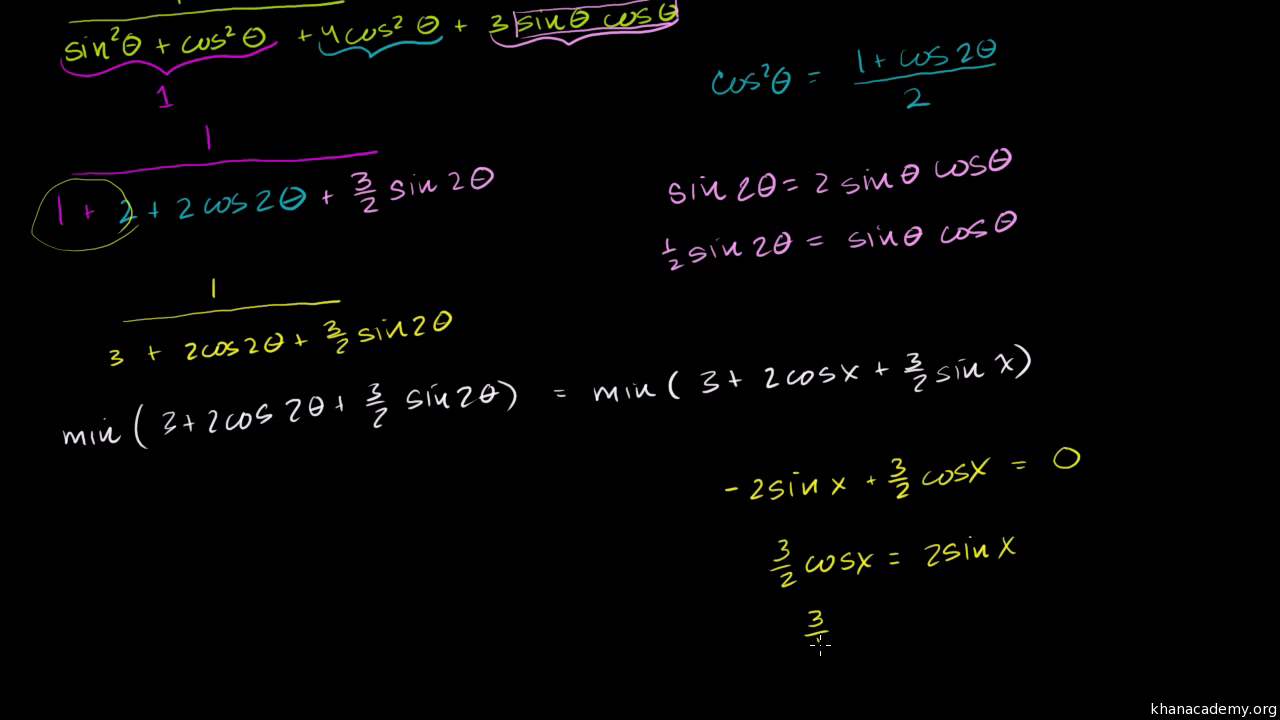


Trig Challenge Problem Maximum Value Video Khan Academy
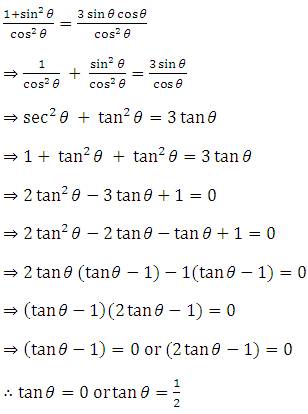


1 Sin2 Theta 3 X Sin Theta X Cos Theta Introduction To Trigonometry Maths Class 10
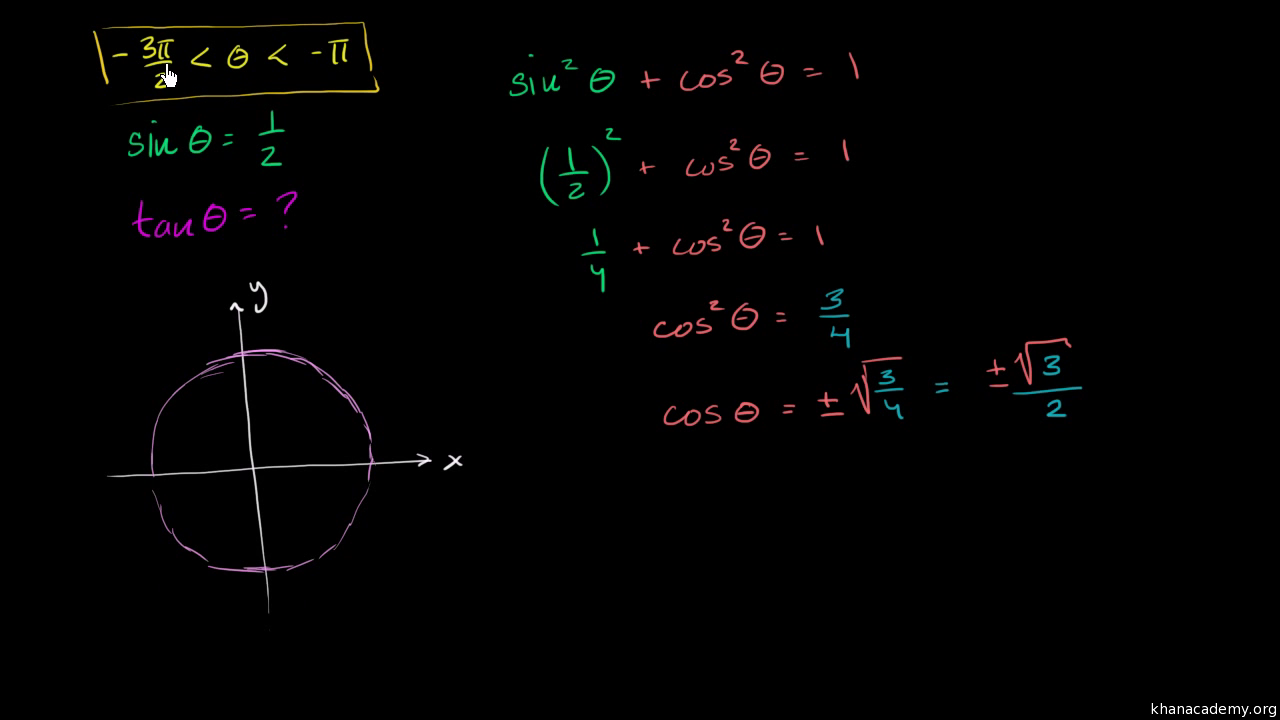


Using The Pythagorean Trig Identity Video Khan Academy



Let F N Theta Tan Theta 2 1 Sec Theta 1 Sec 2theta 1 Sec 2 Ntheta Then Youtube



If Tan Theta Sec 2alpha Prove That Sin2theta 1 Tan 4alpha 1



How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic



Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Th
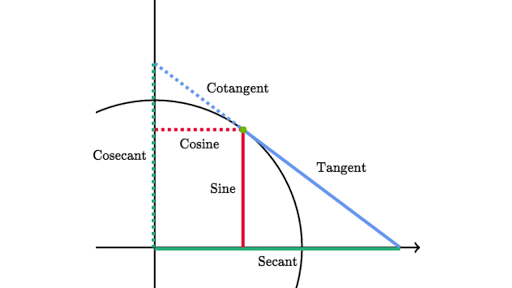


Trig Identity Reference Article Khan Academy



That Tan 3 Theta 1 Tan 2 Theta Cot 3 Theta 1 Cot 2 Theta Sec Theta Csc Theta 2 Sin Theta Cos Theta


Cbse 10 Math Cbse Introduction To Trigonometry Ncert Solutions



Prove That Sec 4theta 1 Sin 4theta 2 Tan 2theta 1



If Theta 30 Verify That Tan 2 Theta 2 Tan Theta 1 Tan Square Theta Brainly In



How To Prove That Tan 5 Theta Tan 3 Theta Tan 5 Theta Tan 3 Theta 4 Cos 2 Theta Cos 4 Theta Quora


Cos 8 3 5 Find Value Of Sin8 1 Tan8 2tan8 Sarthaks Econnect Largest Online Education Community



Tangent Half Angle Formula Wikipedia



Yrvo Lyf7j 5zm
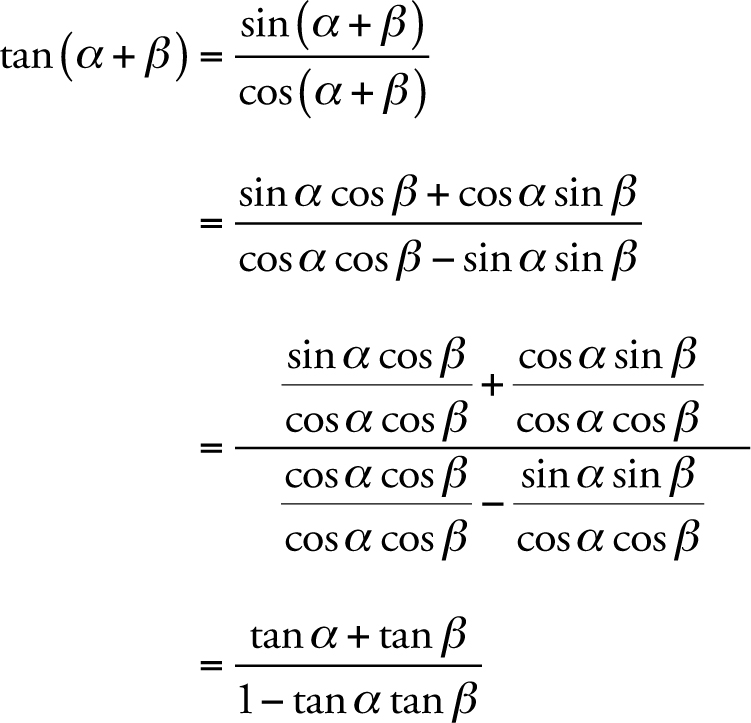


Tangent Identities



If Theta Is An Acute Angles Such That Cos Theta Equal To 3 5 Then Sin Theta Tan Theta Minus 1 Maths Introduction To Trigonometry Meritnation Com



Prove That Tan 3 Theta 1 Tan 2theta Cot 3 Theta 1 Cot 2 Theta
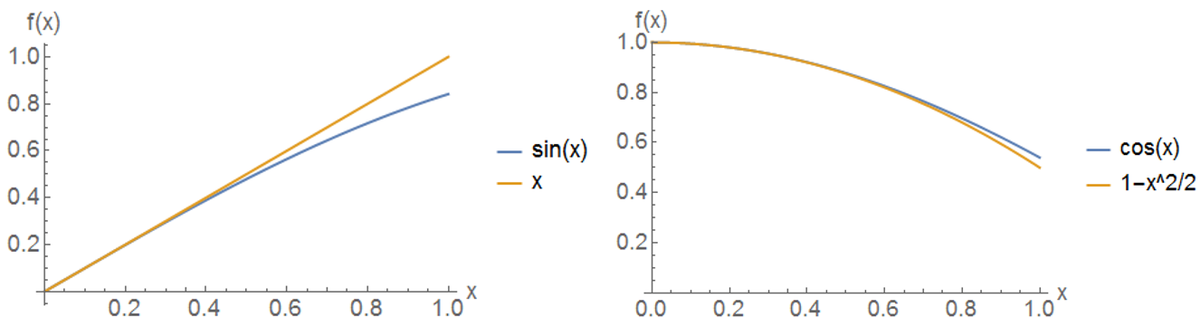


Small Angle Approximation Brilliant Math Science Wiki



If Tan Theta 1 3 Then Evaluate Cosec 2 Theta Sec 2 Theta Cosec 2 Theta Sec 2 Edurev Class 10 Question



If Sec Tita X 1 4x Sec Tita Tan Tita 2x Or 1 2x Mathematics Topperlearning Com 15o2fj


Can You Prove That Math Frac 1 Tan 2 Theta Cot 2 Theta 1 Tan 2 Theta Math Quora


The Trigonometric Ratios Of Angl



What Is Tan 2 Theta Equal To



Trigonometric Identities Topics In Trigonometry



Simplify 1 Tan Squared Theta 1 Sin Theta 1 Sin Theta Brainly In
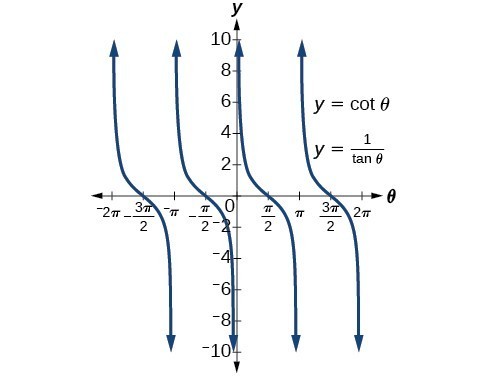


Solving Trigonometric Equations With Identities Precalculus Ii



Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2



If Theta 30 Verify That I Cos2theta 1 Tan 2theta 1


What Is Tan Squared Equal To



If Tan Theta Sec Theta 2 Then What Is Tan Theta Is Equal To Quora



1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube


Prove P2 1 P2 1 Sin Theta Introduction To Trigonometry Maths Class 10


The Trigonometric Ratios Of Angl
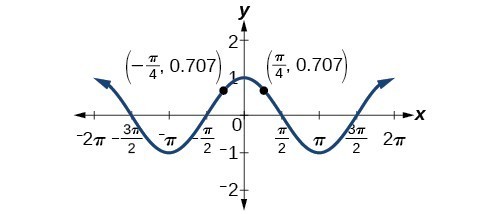


Solving Trigonometric Equations With Identities Precalculus Ii



Cos Squared Theta Minus Sin Square Theta Equal To 1 Minus 10 Squared Theta By 1 10 Squared Theta Prove The Identity Class Of Achievers



If Tan Theta 1 Upon 10 Theta Equals To 2 Then Find The Value Of Tan Square Theta 1 Upon 10 Square Brainly In



Trigonometric Identities


If M Cos8 Sin8 And N Cos8 Sin8 Then Show That M N N M 2 1 Tan 2 8 Sarthaks Econnect Largest Online Education Community


The Trigonometric Ratios Of Angl



Ex 8 2 2 I 2 Tan 30 1 Tan 2 30 With Video Teachoo


If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora



Show That Tan Theta 2 2 Tan Theta 1 5 Tan Theta 2 Sec 2 Theta Brainly In



F Cot Theta Tan Theta X And Sec Theta Cos Theta Y Then Show That Sin Theta Cdot Cos Theta Frac



Tan Theta 1 Cot Theta Cot Theta Divided By 1 Minus 10 Theta Equal To 1 Secant Theta Into Cos Youtube



Tangent Half Angle Formula Wikipedia



Sec Theta Minus Tan Theta By Sin Theta Tan Theta Equal To 1 2 Tan Squared Theta Minus Maths Introduction To Trigonometry Meritnation Com



Tan 2 Theta Sec Theta 1 2 1 Cos Theta 1 Cos Theta Youtube



Solutions To Practice Problems Trig Without Tears


Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Theta Tan 3theta Tan Theta Youtube



Trig Challenge Problem Maximum Value Video Khan Academy


Content Graphing The Trigonometric Functions



Tan Theta Cot Theta Sin Theta Cos Theta Tan 2 Theta Cot 2 Theta Class Of Achievers



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
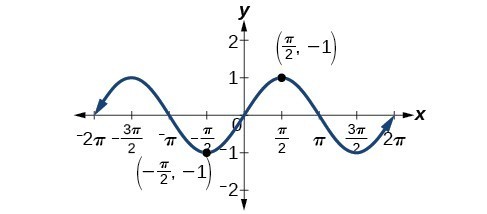


Solving Trigonometric Equations With Identities Precalculus Ii



Tan 2 Theta Cos 2 Theta 1 Cos 2 Theta Brainly In



Prove That Cot 8 Tan 8 2 Cos 2 8 1 Sin 8 Cos 8
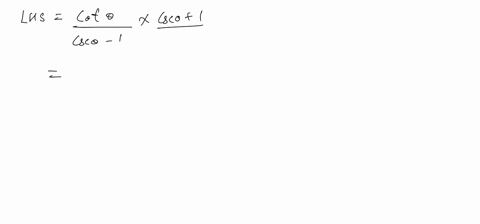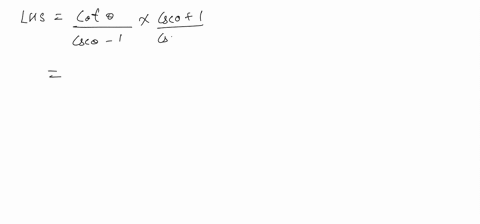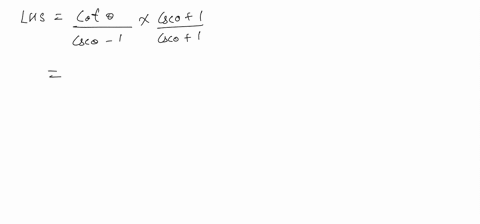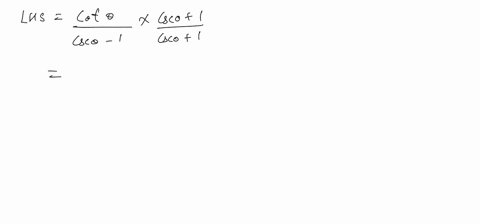


Solved Show That Sec Theta 1 Sec Theta 1



If Theta 60 Then 1 Tan 2 Theta 2tan Theta Is Equal To
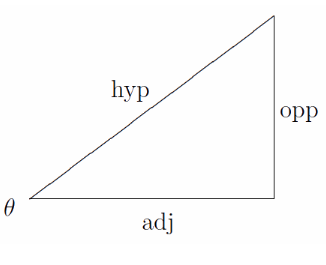


Tan Theta Formula In Trigonometry With Solved Examples



If X A Sec 8 Y B Tan 8 Find D 2y Dx 2 At X P 6 Teachoo



If 41 Sin Theta 40 Evaluate Tan Theta 1 Tan Square Theta Maths Introduction To Trigonometry Meritnation Com



Tangent Half Angle Formula Wikipedia


The Value Of 1 Tan2 15 1 Tan2 15 Is Studyrankersonline



Prove That 1 Tan 28 1 Cot 28 1 Tan8 1 Cot8 2 Tan 28
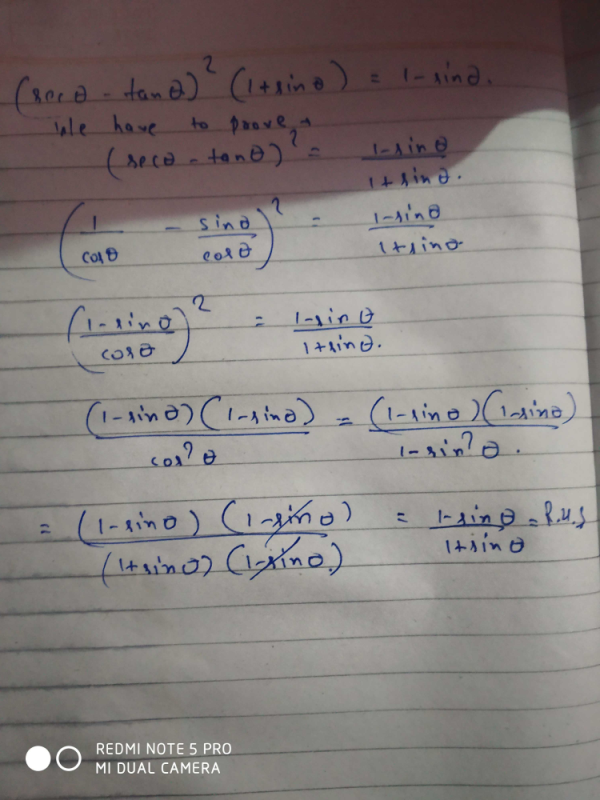


Prove That Sec Theta Tan Theta Square 1 Sin Theta 1 Sin Theta Edurev Class 10 Question



Small Angle Approximation Wikipedia
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com



Theta Tan 1 2 Tan 2 Theta Tan 1 1 3 Tan Theta
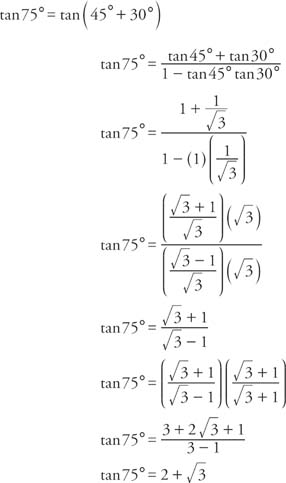


Tangent Identities



No comments:
Post a Comment